Sundials is a collection of six numeric solvers: CVODE, CVODES, IDA, IDAS, ARKODE, and KINSOL [1]. It is written by Cody J. Balos, David J. Gardner, Alan C. Hindmarsh, Daniel R. Reynolds, and Carol S. Woodward at the Center for Applied Scientific Computing, Lawrence Livermore National Laboratory with significant contributions from Radu Serban, and contributions from James Almgren-Bell, Lawrence E. Banks, Peter N. Brown, George Byrne, Rujeko Chinomona, Scott D. Cohen, Aaron Collier, Keith E. Grant, Steven L. Lee, Shelby L. Lockhart, John Loffeld, Daniel McGreer, Slaven Peles, Cosmin Petra, H. Hunter Schwartz, Jean M. Sexton, Dan Shumaker, Steve G. Smith, Allan G. Taylor, Hilari C. Tiedeman, Chris White, Ting Yan, and Ulrike M. Yang.
This OCaml interface was written by Timothy Bourke (Inria/ENS), Jun Inoue (AIST), and Marc Pouzet (UPMC/ENS/Inria). It provides an OCaml interface to most features of Sundials version 6.1.0. There is no support for nvectors based on CUDA, Hypre ParVector, PETSC, RAJA, Trilinos, HIP, or SYCLC; nor for linear solvers requiring CUDA, PETSCSNES, MAGMA, or SuperLU_DIST; nor for XBraid. These features require libraries that are not available in OCaml—contact us if you need them.
The source code is available under a New BSD license at git@github.com:inria-parkas/sundialsml.git. Feedback, bug reports, and pull requests are welcome. Support requests should be made to the OCaml mailing list.
We presented Sundials/ML at the 2016 The OCaml Users and Developers Workshop. A brief technical summary is included in the proceedings of the 2016 ACM Workshop on ML [2]. A greatly extended overview and technical description is included in the Electronic Proceedings in Theoretical Computer Science [3].
Contents
- Overview
- API Reference
- Installation
- Running programs
- Performance
- References
- Acknowledgements
- Indexes
Overview
This interface provides access to the Cvode, Cvodes, Ida, Idas,
Kinsol, and Arkode modules.
Its structure mostly follows that of the original library,
both for ease of reading the official documentation and for converting
existing source code, but several changes have been made for programming
convenience and to increase safety, namely:
- solver sessions are mostly configured via algebraic data types rather than multiple function calls;
- errors are signalled by exceptions, not return codes;
- user data is shared between callback routines via closures (partial function applications);
- vectors are checked for compatibility using a combination of static and dynamic checks; and
- explicit free commands are not necessary since OCaml is a garbage-collected language.
Functions have been renamed according to a regular scheme. Leading module identifiers are replaced by module paths, words
beginning with an uppercase letter are separated by underscores and put
into lowercase. For instance, IdaSetErrHandlerFn, becomes
Ida.set_err_handler_fn, and CVSpilsSetJacTimes becomes
Cvode.Spils.set_jac_times.
Constants are replaced by variant types in most cases. They are renamed by
conversion to CamlCase and the removal of underscores. For instance,
SUN_PREC_NONE becomes
PrecNone.
The names chosen for exceptions sometimes differ from the corresponding return
code names when this improves consistency or comprehensibility.
For instance, the return codes CV_FIRST_RHSFUNC_ERR and
IDA_FIRST_RES_FAIL become, respectively, the exceptions
Cvode.FirstRhsFuncFailure and Ida.FirstResFuncFailure, and CV_BAD_IS
becomes Cvodes.Sensitivity.BadSensIdentifier.
Rather than duplicate the comprehensive Sundials user manuals, this documentation provides brief summaries with references to the original texts and underlying functions.
Nvectors
Sundials defines an abstract interface for vectors and provides
several instantiations.
The OCaml interface defines likewise a generic
Nvector.t type whose type arguments indicate the underlying data and kind.
The Nvector.unwrap function gives direct access to the underlying data.
The interface to serial nvectors, Nvector_serial, is based on
Bigarrays.
These arrays are manipulated directly, i.e., with no additional overhead,
within the solver by the original low-level serial nvector operations
(see Nvector.NVECTOR_OPS).
The same low-level operations can be called from OCaml
(Nvector_serial.Ops), as can equivalent OCaml reimplementations on the
underlying data (Nvector_serial.DataOps).
The interface to parallel nvectors, Nvector_parallel, is based on
Bigarrays
and the OCamlMPI
library. Parallel nvectors are only available when Sundials/ML is configured
to build with MPI.
The Nvector.any type provides alternatives to the standard nvector types.
It replaces the static typing of the data and kind arguments with
dynamic checks on the extensible Nvector.gdata type. This approach is
exploited in the many nvectors, like Nvector_many,
Nvector_mpimany, or Nvector_mpiplusx, that group and operate on arrays
of nvectors.
Besides the standard implementations, it is also possible to define
new nvector implementations through Nvector_custom by providing low-level
operations on an underlying datatype. A demonstration of this feature on
float arrays is provided in Nvector_array. Custom nvectors suffer two
disadvantages compared to the standard nvector implementations. First, each
low-level operation incurs the cost of a callback into OCaml. Second, of all
the provided linear solvers, only Cvode.Diag can be used; although it is
also possible to implement custom solvers in OCaml.
Matrices
Sundials defines an abstract interface for matrices and provides dense, banded, and sparse (either in compressed-sparse-column or compressed-sparse-row format) implementations. The OCaml interface defines likewise a generic Matrix.t type whose type arguments indicate the underlying matrix content and the data and kind of nvectors used in the Matrix.matvec operation. There are specific submodules for dense, band, and sparse content. It is also possible to define custom matrix types by providing a set of standard matrix operations to the Matrix.wrap_custom function. Some low-level matrix routines on arrays are provided by Matrix.ArrayDense and Matrix.ArrayBand.
Nonlinear Solvers
Nonlinear algebraic systems occur optionally in the solution of ODE initial
value problems with Cvode, invariably when solving DAE initial value
problems with Ida, and when solving implicit problems or problems
involving a mass matrix with Arkode.
Sundials provides generic Newton and
Fixed-point nonlinear solvers.
It is also possible to define Custom
nonlinear solvers by providing appropriate OCaml functions.
The user of a nonlinear solver, whether a Sundials module or OCaml program, provides callback functions that describe the system, the setup and solution of linear equations, and a convergence test. It then invokes the setup and solve functions.
Linear Solvers
Sundials.NonlinearSolvers and the Kinsol solver both require the
solution of systems of linear equations for which Sundials provides four
options:
- The diagonal approximation of Jacobians by difference equations (only
for
Cvode); - Direct Linear Solvers (DLS) requiring user-supplied callback functions that explicitly compute a Jacobian;
- Scaled Preconditioned Iterative Linear Solvers (SPILS) requiring user-supplied callback functions to setup and solve linear preconditioning systems;
- Custom linear solvers defined by a set of OCaml functions.
The DLS routines are only available to sessions that use serial, Pthreads, or OpenMP nvectors. The external SuperLU_MT and KLU libraries are required for working with sparse Jacobians. Callback functions manipulate Jacobian matrices through the operations in Matrix.Dense, Matrix.Band, and Matrix.Sparse.
The SPILS routines include the
Scaled Preconditioned GMRES (SPGMR), Scaled Preconditioned Bi-CGStab (SPBCG), Scaled Preconditioned TFQMR
(SPTFQMR), Scaled Preconditioned Flexible GMRES (SPFGMR), and
Preconditioned Conjugate Gradient (PCG) methods.
Additionally, Cvode provides banded preconditioners
for sessions that use serial, Pthreads, or OpenMP nvectors.
Access to the underlying solver
routines on bigarrays is provided via the submodules of
LinearSolver.Iterative.Algorithms.
Parallel Band-Block-Diagonal (BBD) preconditioners are available to sessions
that use parallel nvectors—see Cvode_bbd, Cvodes_bbd, Ida_bbd,
Idas_bbd, and Kinsol_bbd.
Using a linear solver requires three steps:
- Create a generic instance of LinearSolver.t
- Use it to instantiate a solver-specific instance, e.g.,
Cvode.linear_solverorCvodes.Adjoint.linear_solver. - Pass the solver-specific instance to appropriate
initorreinitfunctions, e.g.,Cvode.initorIda.reinit, to create or configure a session.
Any given generic instance, and hence a solver-specific instance, of a linear solver can only be associated with one solver session.
Custom linear solvers can be created by providing a set of operations to LinearSolver.Custom.make_dls, LinearSolver.Custom.make_with_matrix, or LinearSolver.Custom.make_without_matrix.
API Reference
| Sundials | Generic definitions, arrays, matrices, linear solvers, nonlinear solvers, and utility functions. |
| Sundials_parallel | Generic definitions for use with MPI. |
| Nvector | Generic nvector types and operations. |
| Nvector_serial | Standard serial nvectors of Sundials. |
| Nvector_parallel | The standard parallel nvectors of Sundials (requires MPI). |
| Nvector_pthreads | The Pthreads nvectors of Sundials (requires pthreads). |
| Nvector_openmp | The OpenMP nvectors of Sundials (requires OpenMP). |
| Nvector_many | The standard many-vector nvectors of Sundials. |
| Nvector_mpimany | The standard mpimany-vector nvectors of Sundials. |
| Nvector_mpiplusx | The standard mpiplusx nvectors of Sundials. |
| Nvector_custom | An interface for creating custom nvectors in OCaml. |
| Nvector_array | A custom nvector based on float arrays. |
| Cvode | Variable-step solution of ODE initial value problems with zero-crossing detection. |
| Cvode_bbd | Parallel band-block-diagonal preconditioners for CVODE (requires MPI). |
| Cvodes | Sensitivity analysis (forward and adjoint) and quadrature equations for CVODE. |
| Cvodes_bbd | Parallel band-block-diagonal preconditioners for CVODES (requires MPI). |
| Ida | Variable-step solution of DAE initial value problems with zero-crossing detection. |
| Ida_bbd | Parallel band-block-diagonal preconditioners for IDA (requires MPI). |
| Idas | Sensitivity analysis (forward and adjoint) and quadrature equations for IDA. |
| Idas_bbd | Parallel band-block-diagonal preconditioners for IDAS (requires MPI). |
| Arkode | Adaptive-step time integration for stiff, nonstiff, and mixed stiff/nonstiff systems of ODE initial value problems with zero-crossing detection. |
| Arkode_bbd | Parallel band-block-diagonal preconditioners for ARKODE (requires MPI). |
| Kinsol | Solves nonlinear systems using Newton-Krylov techniques. |
| Kinsol_bbd | Parallel band-block-diagonal preconditioners for KINSOL (requires MPI). |
Installation
The dependencies of Sundials/ML are
- OCaml 4.03.0 or greater,
- Sundials 6.1.0 (compiles with version back to 2.7.0 with less features),
- Optionally: OCamlMPI 1.05.
Normally, to install Sundials/ML, you need only type
opam install sundialsml.
The following sections provide more detailed information on building and installing Sundials and Sundials/ML.
Installing Sundials/ML with OPAM
The OPAM package manager provides the easiest way
to install Sundials/ML and the underlying Sundials library.
The features available in Sundials/ML depend on the version and options of
the underlying library (see Sundials.Config).
- Optionally run
opam install mpi. - Run
opam depext sundialsml. - Run
opam install sundialsml.
If OPAM fails to install the required Sundials package automatically, then try using your system's package manager directly, for example:
- Debian/Ubuntu:
apt-get install libsundials-dev - Fedora:
dnf install lapack-devel sundials-devel
sundials-threads-devel sundials-openmpi-devel - macOS:
brew install sundials/port install sundials
Otherwise, the following section describes how to install Sundials
manually.
After installing Sundials, retry opam install sundialsml.
Manually Building and Installing Sundials
First
download
the Sundials source code.
It must be compiled with 64-bit floats (the default: --with-precision=double) and the C compiler must provide 32-bit
ints.
Building the extra features of Sundials requires the installation of dependencies and the right cmake incantation. In particular, it can be tricky to get the optional SuperLU/MT library to work.
For Debian-based systems, we found the following worked:
apt-get install cmake liblapack-dev libopenmpi-dev libsuitesparse-dev
- Optionally download and build SuperLU/MT 3.1.
mkdir build; cd build
cmake -Wno-dev ../sundials-6.1.0 \ -DCMAKE_BUILD_TYPE=Release \ -DOPENMP_ENABLE=1 \ -DPTHREAD_ENABLE=1 \ -DMPI_ENABLE=1 \ -DKLU_ENABLE=1 -DKLU_LIBRARY_DIR=/usr/lib/x86_64-linux-gnu \ -DKLU_INCLUDE_DIR=/usr/include/suitesparse
adding, optionally,-DLAPACK_ENABLE=1 -DLAPACK_LIBRARIES='-llapack -lblas'
adding, if necessary,-DSUPERLUMT_ENABLE=1 \ -DSUPERLUMT_LIBRARY_DIR=<full-path-to>/SuperLU_MT_3.1/lib \ -DSUPERLUMT_INCLUDE_DIR=<full-path-to>/SuperLU_MT_3.1/SRC \ -DSUPERLUMT_LIBRARIES=-lblas
- Build and install Sundials by running
make -j install. - Change to the Sundials/ML source directory and run
./configure
Adding, if necessary,SUPERLUMT_INCLUDE_DIR=<full-path-to>/SuperLU_MT_3.1/SRC \ SUPERLUMT_LIBRARY_DIR=<full-path-to>/SuperLU_MT_3.1/lib \ KLU_INCLUDE_DIR=/usr/include/suitesparse
Note thatSUPERLUMT_LIBRARY_DIRmust be registered withld:export LD_LIBRARY_PATH=<full-path-to>/SuperLU_MT_3.1/lib:$LD_LIBRARY_PATH
- Run
maketo build the library andmake installormake install-findlibto install it.
For macOS, we found the following worked:
- Optionally install
suite-sparse with
brew install suite-sparse. - Optionally download and build SuperLU/MT.
mkdir build; cd build
- For OpenMP, the gcc compiler is required:
cmake -Wno-dev ../sundials-6.1.0 \ -DCMAKE_BUILD_TYPE=Release \ -DCMAKE_C_COMPILER=gcc-11 \ -DOPENMP_ENABLE=1 \ -DPTHREAD_ENABLE=1 \ -DMPI_ENABLE=1 \ -DKLU_ENABLE=1 -DKLU_LIBRARY_DIR=/usr/local/lib -DKLU_INCLUDE_DIR=/usr/local/include
adding, optionally,-DLAPACK_ENABLE=1
adding, if necessary,-DSUPERLUMT_ENABLE=1 \ -DSUPERLUMT_LIBRARY_DIR=<full-path-to>/SuperLU_MT_3.1/lib \ -DSUPERLUMT_INCLUDE_DIR=<full-path-to>/SuperLU_MT_3.1/SRC
- Configure Sundials/ML with
./configure SUPERLUMT_DIR=<full-path-to>/SuperLU_MT_3.1
The Sundials/ML configure script detects and automatically enables optional
features. Lapack solvers, like
LinearSolver.Direct.lapack_dense, are enabled
if Sundials was built with lapack support
(see also Sundials.Config.lapack_enabled).
The KLU and SuperLU_MT solvers, and the Pthreads and OpenMP nvectors are
only enabled if Sundials was built with them.
Parallel nvectors and Band-Block-Diagonal (BBD) solvers
are only enabled if Sundials was built with them and OCamlMPI is available.
Manually Building and Installing Sundials/ML
Building Sundials/ML from source is a three step process:
- Download
and manually install Sundials,
or use a package manager:
- Debian/Ubuntu (without parallelism):
apt-get install libsundials-serial-dev - macOS:
brew install sundials/port install sundials
- Debian/Ubuntu (without parallelism):
- Run
configureto find and check dependencies. - Run
make -j installormake -j install-findlibto build and install the library.
The choices made by the configure script can be influenced by
arguments (like --prefix=...) and variables (like
OCAMLROOT=...). Type configure --help for detailed information.
OCaml reimplementations of the standard Sundials examples are provided in
the examples/ subdirectory.
The library's behaviour can be tested via make -j tests.opt.log which runs the OCaml
versions and compares their outputs against those of the original C
versions: they should be identical.
The library's performance can be analyzed via make perf-intv.opt.pdf which
produces the graph explained below.
The OPAM “pinning” feature is supported: perform step 1 above and then, from the Sundials/ML source directory, run
opam pin add .
Environment variables (SUPERLUMT_LIBRARY_DIR, etc.) can be set to fine-tune
the build process.
Running programs
Compiling and linking
Programs are compiled by specifying where Sundials/ML is installed, e.g.,
-I +sundialsml,- or
-I `opam config var lib`/sundialsml, - or
ocamlfind ... -package sundialsml,
and including bigarray.cma and sundials.cma, for example:
ocamlc -o myprog.byte -I +sundialsml bigarray.cma sundials.cma myprog.ml
or the .cmxa versions:
ocamlopt -o myprog.opt -I +sundialsml bigarray.cmxa sundials.cmxa myprog.ml
The sundials.cma/.cmxa files link against the libraries
libsundials_cvodes and libsundials_idas. The code in these libraries
should give the same results as that in those without sensitivity analysis
(except for the functions Cvode.get_work_space and Ida.get_work_space),
even though they are compiled from distinct source files. The
sundials_no_sens.cma/cmxa files, on the other hand, link against the
libraries libsundials_cvode and libsundials_ida and thus do not include the
functionality in Cvodes or Idas.
Both sets of files link against
libsundials_kinsol, libsundials_arkode, and libsundials_nvecserial.
The parallel features—in the Nvector_parallel, Cvode_bbd,
Cvodes_bbd, Ida_bbd, Idas_bbd, Kinsol_bbd, and Arkode_bbd
modules—require the
additional inclusions of mpi.cma and sundials_mpi.cma. So, for example:
ocamlc -o myprog.byte -I +sundialsml bigarray.cma mpi.cma sundials.cma \ sundials_mpi.cma myprog.ml
or with the .cmxa versions:
ocamlopt -o myprog.opt -I +sundialsml bigarray.cmxa mpi.cmxa sundials.cmxa \ sundials_mpi.cmxa myprog.ml
The sundials_mpi.cm(x)a files link against the
libsundials_nvecparallel library.
The Nvector_openmp and Nvector_pthreads modules require the additional
inclusion, respectively, of sundials_openmp.cm(x)a and
sundials_pthreads.cm(x)a.
Under ocamlfind, the parallel, OpenMP, and Pthreads features
are selected via subpackages, and the use of the libraries without
sensitivity analysis via a predicate.
For example, for everything:
ocamlfind ocamlopt -package sundialsml.mpi,sundials.pthreads,sundials.openmp \ -linkpkg -o mysim.opt mysim.ml
The available packages and the features they select are:
sundialsml: basic features; add-predicates no_sensto disable sensitivity,sundialsml.mpi: additionally include MPI-based parallel nvectors,sundialsml.openmp: additionally include OpenMP nvectors,sundialsml.pthreads: additionally include Pthreads nvectors.
From the toplevel
Sundials/ML can also be used from the OCaml interactive loop, either by an invocation like:
ocaml bigarray.cma -I +sundialsml sundials.cma
or through ocamlfind, for example:
#use "topfind";;
#predicates "no_sens";; (* optional: excludes sensitivity code *)
#require "sundialsml";;
let f t y yd = yd.{0} <- 1.;;
let g t y gout = gout.{0} <- y.{0};;
let y = Sundials.RealArray.of_array [| -1.0 |];;
let yvec = Nvector_serial.wrap y;;
let s = Cvode.(init Adams default_tolerances f ~roots:(1, g) 0. yvec);;
Cvode.set_stop_time s 2.;;
(* repeat the commands below to advance the simulation until t = 2.0 *)
let (t', result) = Cvode.solve_normal s 2. yvec;;
Format.printf "%e: %a\n" t' Sundials.RealArray.pp y;;Using MPI from a toplevel is best done with ocamlfind by first creating a
custom toplevel:
ocamlfind ocamlmktop -o partop -package sundialsml.mpi,findlib -linkpkg
and then launching it in multiple terminals:
mpirun -np 2 xterm -e ./partop
Here, 2 is the number of processes, xterm is the terminal program, and
-e ./partop has each xterm execute ./partop.
As a simple test, paste the following into all terminals:
#use "topfind";;
#require "sundialsml.mpi";;
let comm = Mpi.comm_world
let n = Mpi.comm_size comm
let my_id = Mpi.comm_rank comm
let pv = Nvector_parallel.make 1 n comm (float_of_int (my_id + 1));;
Printf.printf "%d: local=%f.\n" my_id (Nvector_parallel.local_array pv).{0};;
Printf.printf "Sum of abs. = %f\n" (Nvector_parallel.Ops.n_vl1norm pv);;
Solutions to common problems
- The message
Fatal error: cannot load required shared library dllmlsundials
can usually be fixed by updatingLD_LIBRARY_PATH, for example,export LD_LIBRARY_PATH=/usr/local/lib:${LD_LIBRARY_PATH}Otherwise you may have compiled Sundials without--enable-shared. - The configuration warning
Couldn't determine C compiler flag for OpenMP.
can usually be eliminated by specifying a compiler that supports OpenMP, for example,CC=gcc-11 ./configure
Performance
An interface like Sundials/ML inevitably adds overhead: there is extra code to execute at each call. But, how significant is this cost? And, more broadly, how does the performance of OCaml compare to that of C for programs that use numeric solvers?
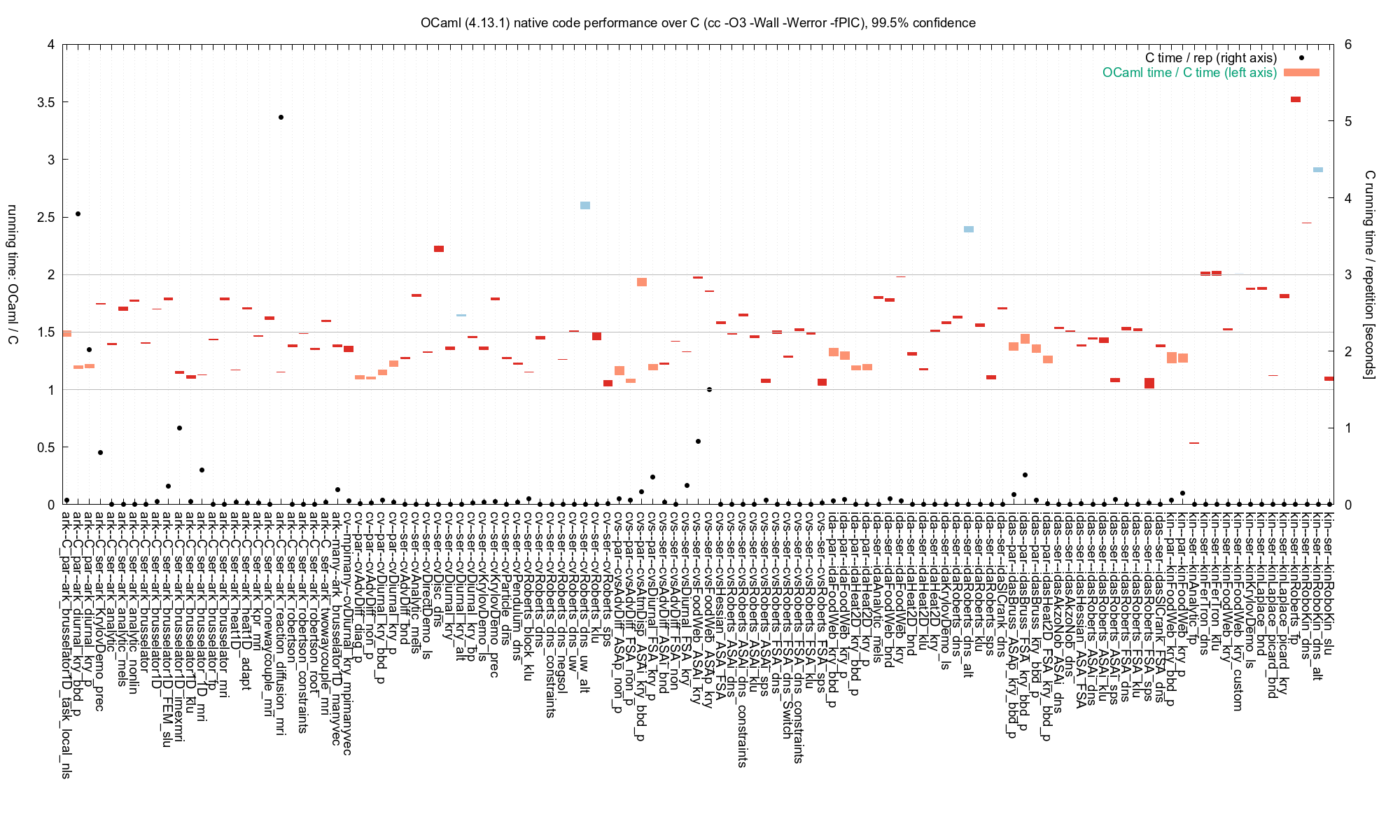
These questions are not easy to answer. As a first attempt, we took the examples in C from the Sundials distribution, reimplemented them in OCaml and compared the execution times. The bars in the graph below show the ratios of the execution times of the OCaml code to the C code, i.e., a value of 2 on the left axis means that OCaml is twice as slow. The black dots indicate, against the right axis, the execution time of the C code.
The colored bars show the confidence intervals of the estimated running times. More precisely, let $C$ and $O$ be random variables representing the running times of an example coded, respectively, in C and OCaml. The plot shows the range of $r$ such that the null hypothesis $P(rC < O) = P(rC > O)$ is not rejected at the 99.5% confidence level.
The graph shows that the OCaml examples are usually
less than 50% slower than the original ones, sometimes up to 100% slower,
and only very rarely any slower than that.
The *_custom example (light blue) uses custom nvectors
with low-level operations in OCaml and the *_alt examples (darker blue) use linear solvers implemented in OCaml.
The OCaml library and examples were compiled in “unsafe” mode, that is,
without array bounds and other safety checks—the C code does not perform
these checks either.
The results with safety checks are also
available.
This conclusion seems reasonable as a first approximation, but several
details of the analysis process and individual results show that the real
situation is less clear-cut. For one, the running times of most of the
examples are so short that accurate profiling is not possible, i.e.,
time
and gprof simply show 0
seconds.
The figures in the graph were obtained by modifying the examples to
repeatedly execute their main functions.
The number of repetitions varies per example since otherwise the slower
examples take too long.
The timings indicated by the dots and the axis at right are calculated by
dividing the wall-clock time of each C version by the number of repetitions.
All but six of the serial examples (red) run so fast that
comparisons are made based on tens, or usually hundreds of repetitions and
in some cases this amplifies factors other than the interface overhead.
The slowest example, for instance, kin--ser--kinRoberts_fp is iterated
nearly 200 000 times to achieve a significant wall clock time.
This means creating and destroying many more data structures than usual for
such code.
In fact, about 25% of the runtime is spent in garbage collection,
about 15% in allocating nvectors (10% in calloc alone),
about 10% in freeing memory on the C heap,
and about 15% calling printf.
There is very little calculation in this example and thus bookkeeping
predominates (and OCaml does more of it than C).
Similar comments apply to the second slowest example,
kin--ser--kinRoboKin_dns (10% in garbage collection and 30% in printf
formatting numbers).
The running times of the parallel examples (lighter red) often vary considerably between different runs. Those with the highest variations—with the exception of idaHeat2D_kry_bbd_p—often have relatively long running times and the results are obtained in relatively few (< 10) iterations.
We were able to make our OCaml versions much faster (up to 4 times) by:
- Adding explicit type annotations to all vector arguments.
For instance, rather than declare a callback with
it is better to uselet f t y yd = ... ,
or more conciselylet f t (y : Sundials.RealArray.t) (yd : Sundials.RealArray.t) = ... ,
since then the compiler need not generate polymorphic code and can optimize for the bigarray layout.let f : Sundials.RealArray.t Cvode.rhsfn = fun t y yd -> ... - Avoid functions like
Bigarray.Array1.subandBigarray.Array2.slice_left. These functions allocate new bigarrays on the major heap, which increases the frequency of major GCs. They can often be avoided by calculating and passing indices more explicitly. When part of an array must be passed to another function, it can be faster, depending on the size, to copy into and out of a statically-allocated temporary array. - Sequences of RealArray2.get and RealArray2.set operations are usually better replaced by RealArray2.unwrap (projection from a tuple) and direct accesses to the underlying array.
- Write numeric expressions and loops according to the advice in [4] to avoid float ‘boxing’.
In summary, OCaml code using the Sundials solvers should almost never be more than 50% slower than the equivalent code written in C, provided the guidelines above are followed, and it should usually not be more than 30% slower. It is usually, however, faster to write and debug OCaml code thanks to automatic memory management, bounds checking on arrays, strong static type checking, higher-order functions, etcetera. Moreover, the Sundials/ML library offers a good comprise for programs combining symbolic manipulation and numeric calculation.
The graph above can be generated from the Sundials source by running
cd examples; make perf-intv.opt.pdf GC_AT_END=1 PERF_DATA_POINTS=40
Be sure to build Sundials with -DCMAKE_BUILD_TYPE=Release otherwise the
underlying library is unoptimized.
Sundials/ML should be configured with -unsafe.
References
- A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S. Woodward, “ SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers,” ACM Transactions on Mathematical Software, 31(3), pp. 363-396, 2005.
- T. Bourke, J. Inoue, and M. Pouzet, “Sundials/ML: interfacing with numerical solvers,” ACM Workshop on ML, Nara, Japan, 2016.
- T. Bourke, J. Inoue, and M. Pouzet, “Sundials/ML: Connecting OCaml to the Sundials Numeric Solvers,” EPTCS 285, pp. 101–130, 2018.
- X. Leroy, “Old Objective Caml site: Writing efficient numerical code in Objective Caml,” July 2002.
Acknowledgements
We gratefully acknowledge the support of the ITEA 3 project 11004 MODRIO (Model driven physical systems operation), Inria (Modeliscale), and the Departement d'Informatique de l'ENS.
This library benefits greatly from the OCaml Bigarray and MPI libraries, and from OCaml's optimized floating-point representations and compilation.
This documentation uses J. Protzenko's CSS stylesheet, and MathJax for rendering mathematics.
We are grateful for direct contributions to this library from