Sundials/ML 6.1.0p0

Sundials is a collection of six numeric solvers: CVODE, CVODES, IDA, IDAS, ARKODE, and KINSOL [1]. It is written by Cody J. Balos, David J. Gardner, Alan C. Hindmarsh, Daniel R. Reynolds, and Carol S. Woodward at the Center for Applied Scientific Computing, Lawrence Livermore National Laboratory with significant contributions from Radu Serban, and contributions from James Almgren-Bell, Lawrence E. Banks, Peter N. Brown, George Byrne, Rujeko Chinomona, Scott D. Cohen, Aaron Collier, Keith E. Grant, Steven L. Lee, Shelby L. Lockhart, John Loffeld, Daniel McGreer, Slaven Peles, Cosmin Petra, H. Hunter Schwartz, Jean M. Sexton, Dan Shumaker, Steve G. Smith, Allan G. Taylor, Hilari C. Tiedeman, Chris White, Ting Yan, and Ulrike M. Yang.

This OCaml interface was written by Timothy Bourke (Inria/ENS), Jun Inoue (AIST), and Marc Pouzet (UPMC/ENS/Inria). It provides an OCaml interface to most features of Sundials version 6.1.0. There is no support for nvectors based on CUDA, Hypre ParVector, PETSC, RAJA, Trilinos, HIP, or SYCLC; nor for linear solvers requiring CUDA, PETSCSNES, MAGMA, or SuperLU_DIST; nor for XBraid. These features require libraries that are not available in OCaml—contact us if you need them.

The source code is available under a New BSD license at git@github.com:inria-parkas/sundialsml.git. Feedback, bug reports, and pull requests are welcome. Support requests should be made to the OCaml mailing list.

We presented Sundials/ML at the 2016 The OCaml Users and Developers Workshop. A brief technical summary is included in the proceedings of the 2016 ACM Workshop on ML [2]. A greatly extended overview and technical description is included in the Electronic Proceedings in Theoretical Computer Science [3].

Contents

Overview

This interface provides access to the Cvode, Cvodes, Ida, Idas, Kinsol, and Arkode modules. Its structure mostly follows that of the original library, both for ease of reading the official documentation and for converting existing source code, but several changes have been made for programming convenience and to increase safety, namely:

Functions have been renamed according to a regular scheme. Leading module identifiers are replaced by module paths, words beginning with an uppercase letter are separated by underscores and put into lowercase. For instance, IdaSetErrHandlerFn, becomes Ida.set_err_handler_fn, and CVSpilsSetJacTimes becomes Cvode.Spils.set_jac_times.

Constants are replaced by variant types in most cases. They are renamed by conversion to CamlCase and the removal of underscores. For instance, SUN_PREC_NONE becomes PrecNone. The names chosen for exceptions sometimes differ from the corresponding return code names when this improves consistency or comprehensibility. For instance, the return codes CV_FIRST_RHSFUNC_ERR and IDA_FIRST_RES_FAIL become, respectively, the exceptions Cvode.FirstRhsFuncFailure and Ida.FirstResFuncFailure, and CV_BAD_IS becomes Cvodes.Sensitivity.BadSensIdentifier.

Rather than duplicate the comprehensive Sundials user manuals, this documentation provides brief summaries with references to the original texts and underlying functions.

Nvectors

Sundials defines an abstract interface for vectors and provides several instantiations. The OCaml interface defines likewise a generic Nvector.t type whose type arguments indicate the underlying data and kind. The Nvector.unwrap function gives direct access to the underlying data.

The interface to serial nvectors, Nvector_serial, is based on Bigarrays. These arrays are manipulated directly, i.e., with no additional overhead, within the solver by the original low-level serial nvector operations (see Nvector.NVECTOR_OPS). The same low-level operations can be called from OCaml (Nvector_serial.Ops), as can equivalent OCaml reimplementations on the underlying data (Nvector_serial.DataOps).

The interface to parallel nvectors, Nvector_parallel, is based on Bigarrays and the OCamlMPI library. Parallel nvectors are only available when Sundials/ML is configured to build with MPI.

The Nvector.any type provides alternatives to the standard nvector types. It replaces the static typing of the data and kind arguments with dynamic checks on the extensible Nvector.gdata type. This approach is exploited in the many nvectors, like Nvector_many, Nvector_mpimany, or Nvector_mpiplusx, that group and operate on arrays of nvectors.

Besides the standard implementations, it is also possible to define new nvector implementations through Nvector_custom by providing low-level operations on an underlying datatype. A demonstration of this feature on float arrays is provided in Nvector_array. Custom nvectors suffer two disadvantages compared to the standard nvector implementations. First, each low-level operation incurs the cost of a callback into OCaml. Second, of all the provided linear solvers, only Cvode.Diag can be used; although it is also possible to implement custom solvers in OCaml.

Matrices

Sundials defines an abstract interface for matrices and provides dense, banded, and sparse (either in compressed-sparse-column or compressed-sparse-row format) implementations. The OCaml interface defines likewise a generic Matrix.t type whose type arguments indicate the underlying matrix content and the data and kind of nvectors used in the Matrix.matvec operation. There are specific submodules for dense, band, and sparse content. It is also possible to define custom matrix types by providing a set of standard matrix operations to the Matrix.wrap_custom function. Some low-level matrix routines on arrays are provided by Matrix.ArrayDense and Matrix.ArrayBand.

Nonlinear Solvers

Nonlinear algebraic systems occur optionally in the solution of ODE initial value problems with Cvode, invariably when solving DAE initial value problems with Ida, and when solving implicit problems or problems involving a mass matrix with Arkode. Sundials provides generic Newton and Fixed-point nonlinear solvers. It is also possible to define Custom nonlinear solvers by providing appropriate OCaml functions.

The user of a nonlinear solver, whether a Sundials module or OCaml program, provides callback functions that describe the system, the setup and solution of linear equations, and a convergence test. It then invokes the setup and solve functions.

Linear Solvers

Sundials.NonlinearSolvers and the Kinsol solver both require the solution of systems of linear equations for which Sundials provides four options:

The DLS routines are only available to sessions that use serial, Pthreads, or OpenMP nvectors. The external SuperLU_MT and KLU libraries are required for working with sparse Jacobians. Callback functions manipulate Jacobian matrices through the operations in Matrix.Dense, Matrix.Band, and Matrix.Sparse.

The SPILS routines include the Scaled Preconditioned GMRES (SPGMR), Scaled Preconditioned Bi-CGStab (SPBCG), Scaled Preconditioned TFQMR (SPTFQMR), Scaled Preconditioned Flexible GMRES (SPFGMR), and Preconditioned Conjugate Gradient (PCG) methods. Additionally, Cvode provides banded preconditioners for sessions that use serial, Pthreads, or OpenMP nvectors. Access to the underlying solver routines on bigarrays is provided via the submodules of LinearSolver.Iterative.Algorithms. Parallel Band-Block-Diagonal (BBD) preconditioners are available to sessions that use parallel nvectors—see Cvode_bbd, Cvodes_bbd, Ida_bbd, Idas_bbd, and Kinsol_bbd.

Using a linear solver requires three steps:

  1. Create a generic instance of LinearSolver.t
  2. Use it to instantiate a solver-specific instance, e.g., Cvode.linear_solver or Cvodes.Adjoint.linear_solver.
  3. Pass the solver-specific instance to appropriate init or reinit functions, e.g., Cvode.init or Ida.reinit, to create or configure a session.

Any given generic instance, and hence a solver-specific instance, of a linear solver can only be associated with one solver session.

Custom linear solvers can be created by providing a set of operations to LinearSolver.Custom.make_dls, LinearSolver.Custom.make_with_matrix, or LinearSolver.Custom.make_without_matrix.

API Reference

Sundials

Generic definitions, arrays, matrices, linear solvers, nonlinear solvers, and utility functions.

Sundials_parallel

Generic definitions for use with MPI.

Nvector

Generic nvector types and operations.

Nvector_serial

Standard serial nvectors of Sundials.

Nvector_parallel

The standard parallel nvectors of Sundials (requires MPI).

Nvector_pthreads

The Pthreads nvectors of Sundials (requires pthreads).

Nvector_openmp

The OpenMP nvectors of Sundials (requires OpenMP).

Nvector_many

The standard many-vector nvectors of Sundials.

Nvector_mpimany

The standard mpimany-vector nvectors of Sundials.

Nvector_mpiplusx

The standard mpiplusx nvectors of Sundials.

Nvector_custom

An interface for creating custom nvectors in OCaml.

Nvector_array

A custom nvector based on float arrays.

Cvode

Variable-step solution of ODE initial value problems with zero-crossing detection.

Cvode_bbd

Parallel band-block-diagonal preconditioners for CVODE (requires MPI).

Cvodes

Sensitivity analysis (forward and adjoint) and quadrature equations for CVODE.

Cvodes_bbd

Parallel band-block-diagonal preconditioners for CVODES (requires MPI).

Ida

Variable-step solution of DAE initial value problems with zero-crossing detection.

Ida_bbd

Parallel band-block-diagonal preconditioners for IDA (requires MPI).

Idas

Sensitivity analysis (forward and adjoint) and quadrature equations for IDA.

Idas_bbd

Parallel band-block-diagonal preconditioners for IDAS (requires MPI).

Arkode

Adaptive-step time integration for stiff, nonstiff, and mixed stiff/nonstiff systems of ODE initial value problems with zero-crossing detection.

Arkode_bbd

Parallel band-block-diagonal preconditioners for ARKODE (requires MPI).

Kinsol

Solves nonlinear systems using Newton-Krylov techniques.

Kinsol_bbd

Parallel band-block-diagonal preconditioners for KINSOL (requires MPI).

Installation

The dependencies of Sundials/ML are

Normally, to install Sundials/ML, you need only type opam install sundialsml.

The following sections provide more detailed information on building and installing Sundials and Sundials/ML.

Installing Sundials/ML with OPAM

The OPAM package manager provides the easiest way to install Sundials/ML and the underlying Sundials library. The features available in Sundials/ML depend on the version and options of the underlying library (see Sundials.Config).

  1. Optionally run opam install mpi.
  2. Run opam depext sundialsml.
  3. Run opam install sundialsml.

If OPAM fails to install the required Sundials package automatically, then try using your system's package manager directly, for example:

Otherwise, the following section describes how to install Sundials manually. After installing Sundials, retry opam install sundialsml.

Manually Building and Installing Sundials

First download the Sundials source code. It must be compiled with 64-bit floats (the default: --with-precision=double) and the C compiler must provide 32-bit ints.

Building the extra features of Sundials requires the installation of dependencies and the right cmake incantation. In particular, it can be tricky to get the optional SuperLU/MT library to work.

For Debian-based systems, we found the following worked:

  1. apt-get install cmake liblapack-dev libopenmpi-dev libsuitesparse-dev
  2. Optionally download and build SuperLU/MT 3.1.
  3. mkdir build; cd build
  4. cmake -Wno-dev ../sundials-6.1.0 \
-DCMAKE_BUILD_TYPE=Release \
-DOPENMP_ENABLE=1 \
-DPTHREAD_ENABLE=1 \
-DMPI_ENABLE=1 \
-DKLU_ENABLE=1 -DKLU_LIBRARY_DIR=/usr/lib/x86_64-linux-gnu \
-DKLU_INCLUDE_DIR=/usr/include/suitesparse
    adding, optionally, 
    -DLAPACK_ENABLE=1 -DLAPACK_LIBRARIES='-llapack -lblas'
    adding, if necessary, 
    -DSUPERLUMT_ENABLE=1 \
-DSUPERLUMT_LIBRARY_DIR=<full-path-to>/SuperLU_MT_3.1/lib \
-DSUPERLUMT_INCLUDE_DIR=<full-path-to>/SuperLU_MT_3.1/SRC \
-DSUPERLUMT_LIBRARIES=-lblas
  5. Build and install Sundials by running make -j install.
  6. Change to the Sundials/ML source directory and run 
    ./configure
    Adding, if necessary, 
    SUPERLUMT_INCLUDE_DIR=<full-path-to>/SuperLU_MT_3.1/SRC \
SUPERLUMT_LIBRARY_DIR=<full-path-to>/SuperLU_MT_3.1/lib \
KLU_INCLUDE_DIR=/usr/include/suitesparse
    Note that SUPERLUMT_LIBRARY_DIR must be registered with ld: 
    export LD_LIBRARY_PATH=<full-path-to>/SuperLU_MT_3.1/lib:$LD_LIBRARY_PATH
  7. Run make to build the library and make install or make install-findlib to install it.

For macOS, we found the following worked:

  1. Optionally install suite-sparse with brew install suite-sparse.
  2. Optionally download and build SuperLU/MT.
  3. mkdir build; cd build
  4. For OpenMP, the gcc compiler is required: 
    cmake -Wno-dev ../sundials-6.1.0 \
-DCMAKE_BUILD_TYPE=Release \
-DCMAKE_C_COMPILER=gcc-11 \
-DOPENMP_ENABLE=1 \
-DPTHREAD_ENABLE=1 \
-DMPI_ENABLE=1 \
-DKLU_ENABLE=1 -DKLU_LIBRARY_DIR=/usr/local/lib -DKLU_INCLUDE_DIR=/usr/local/include
    adding, optionally, 
    -DLAPACK_ENABLE=1
    adding, if necessary, 
    -DSUPERLUMT_ENABLE=1 \
-DSUPERLUMT_LIBRARY_DIR=<full-path-to>/SuperLU_MT_3.1/lib \
-DSUPERLUMT_INCLUDE_DIR=<full-path-to>/SuperLU_MT_3.1/SRC
  5. Configure Sundials/ML with 
    ./configure SUPERLUMT_DIR=<full-path-to>/SuperLU_MT_3.1

The Sundials/ML configure script detects and automatically enables optional features. Lapack solvers, like LinearSolver.Direct.lapack_dense, are enabled if Sundials was built with lapack support (see also Sundials.Config.lapack_enabled). The KLU and SuperLU_MT solvers, and the Pthreads and OpenMP nvectors are only enabled if Sundials was built with them. Parallel nvectors and Band-Block-Diagonal (BBD) solvers are only enabled if Sundials was built with them and OCamlMPI is available.

Manually Building and Installing Sundials/ML

Building Sundials/ML from source is a three step process:

  1. Download and manually install Sundials, or use a package manager:
    • Debian/Ubuntu (without parallelism): apt-get install libsundials-serial-dev
    • macOS: brew install sundials / port install sundials
  2. Run configure to find and check dependencies.
  3. Run make -j install or make -j install-findlib to build and install the library.

The choices made by the configure script can be influenced by arguments (like --prefix=...) and variables (like OCAMLROOT=...). Type configure --help for detailed information.

OCaml reimplementations of the standard Sundials examples are provided in the examples/ subdirectory. The library's behaviour can be tested via make -j tests.opt.log which runs the OCaml versions and compares their outputs against those of the original C versions: they should be identical. The library's performance can be analyzed via make perf-intv.opt.pdf which produces the graph explained below.

The OPAM “pinning” feature is supported: perform step 1 above and then, from the Sundials/ML source directory, run

opam pin add .

Environment variables (SUPERLUMT_LIBRARY_DIR, etc.) can be set to fine-tune the build process.

Running programs

Compiling and linking

Programs are compiled by specifying where Sundials/ML is installed, e.g.,

and including bigarray.cma and sundials.cma, for example:

ocamlc -o myprog.byte -I +sundialsml bigarray.cma sundials.cma myprog.ml

or the .cmxa versions:

ocamlopt -o myprog.opt -I +sundialsml bigarray.cmxa sundials.cmxa myprog.ml

The sundials.cma/.cmxa files link against the libraries libsundials_cvodes and libsundials_idas. The code in these libraries should give the same results as that in those without sensitivity analysis (except for the functions Cvode.get_work_space and Ida.get_work_space), even though they are compiled from distinct source files. The sundials_no_sens.cma/cmxa files, on the other hand, link against the libraries libsundials_cvode and libsundials_ida and thus do not include the functionality in Cvodes or Idas. Both sets of files link against libsundials_kinsol, libsundials_arkode, and libsundials_nvecserial.

The parallel features—in the Nvector_parallel, Cvode_bbd, Cvodes_bbd, Ida_bbd, Idas_bbd, Kinsol_bbd, and Arkode_bbd modules—require the additional inclusions of mpi.cma and sundials_mpi.cma. So, for example:

ocamlc -o myprog.byte -I +sundialsml bigarray.cma mpi.cma sundials.cma \
					sundials_mpi.cma myprog.ml

or with the .cmxa versions:

ocamlopt -o myprog.opt -I +sundialsml bigarray.cmxa mpi.cmxa sundials.cmxa \
					 sundials_mpi.cmxa myprog.ml

The sundials_mpi.cm(x)a files link against the libsundials_nvecparallel library.

The Nvector_openmp and Nvector_pthreads modules require the additional inclusion, respectively, of sundials_openmp.cm(x)a and sundials_pthreads.cm(x)a.

Under ocamlfind, the parallel, OpenMP, and Pthreads features are selected via subpackages, and the use of the libraries without sensitivity analysis via a predicate. For example, for everything:

ocamlfind ocamlopt -package sundialsml.mpi,sundials.pthreads,sundials.openmp \
				-linkpkg -o mysim.opt mysim.ml

The available packages and the features they select are:

From the toplevel

Sundials/ML can also be used from the OCaml interactive loop, either by an invocation like:

ocaml bigarray.cma -I +sundialsml sundials.cma

or through ocamlfind, for example:

#use "topfind";;
#predicates "no_sens";;	  (* optional: excludes sensitivity code *)
#require "sundialsml";;

let f t y yd = yd.{0} <- 1.;;
let g t y gout = gout.{0} <- y.{0};;
let y = Sundials.RealArray.of_array [| -1.0 |];;
let yvec = Nvector_serial.wrap y;;
let s = Cvode.(init Adams default_tolerances f ~roots:(1, g) 0. yvec);;
Cvode.set_stop_time s 2.;;

(* repeat the commands below to advance the simulation until t = 2.0 *)
let (t', result) = Cvode.solve_normal s 2. yvec;;
Format.printf "%e: %a\n" t' Sundials.RealArray.pp y;;

Using MPI from a toplevel is best done with ocamlfind by first creating a custom toplevel:

ocamlfind ocamlmktop -o partop -package sundialsml.mpi,findlib -linkpkg

and then launching it in multiple terminals:

mpirun -np 2 xterm -e ./partop

Here, 2 is the number of processes, xterm is the terminal program, and -e ./partop has each xterm execute ./partop. As a simple test, paste the following into all terminals:

#use "topfind";;
#require "sundialsml.mpi";;

let comm = Mpi.comm_world
let n = Mpi.comm_size comm
let my_id = Mpi.comm_rank comm
let pv = Nvector_parallel.make 1 n comm (float_of_int (my_id + 1));;

Printf.printf "%d: local=%f.\n" my_id (Nvector_parallel.local_array pv).{0};;
Printf.printf "Sum of abs. = %f\n" (Nvector_parallel.Ops.n_vl1norm pv);;

Solutions to common problems

  1. The message 
    Fatal error: cannot load required shared library dllmlsundials
    can usually be fixed by updating LD_LIBRARY_PATH, for example, 
    export LD_LIBRARY_PATH=/usr/local/lib:${LD_LIBRARY_PATH}
    Otherwise you may have compiled Sundials without --enable-shared.
  2. The configuration warning 
    Couldn't determine C compiler flag for OpenMP.
    can usually be eliminated by specifying a compiler that supports OpenMP, for example, 
    CC=gcc-11 ./configure

Performance

An interface like Sundials/ML inevitably adds overhead: there is extra code to execute at each call. But, how significant is this cost? And, more broadly, how does the performance of OCaml compare to that of C for programs that use numeric solvers?

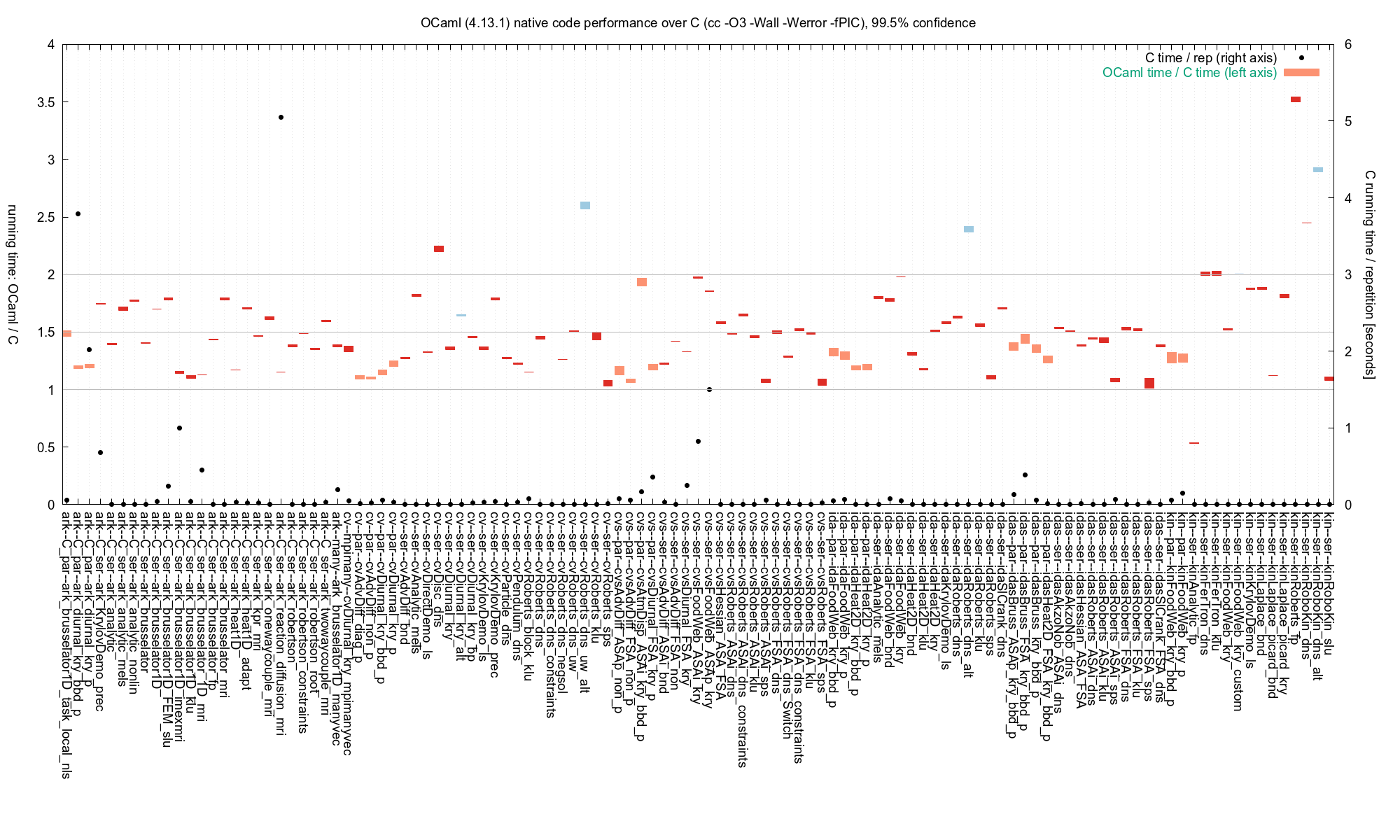
These questions are not easy to answer. As a first attempt, we took the examples in C from the Sundials distribution, reimplemented them in OCaml and compared the execution times. The bars in the graph below show the ratios of the execution times of the OCaml code to the C code, i.e., a value of 2 on the left axis means that OCaml is twice as slow. The black dots indicate, against the right axis, the execution time of the C code.

The colored bars show the confidence intervals of the estimated running times. More precisely, let $C$ and $O$ be random variables representing the running times of an example coded, respectively, in C and OCaml. The plot shows the range of $r$ such that the null hypothesis $P(rC < O) = P(rC > O)$ is not rejected at the 99.5% confidence level.

The graph shows that the OCaml examples are usually less than 50% slower than the original ones, sometimes up to 100% slower, and only very rarely any slower than that. The *_custom example (light blue) uses custom nvectors with low-level operations in OCaml and the *_alt examples (darker blue) use linear solvers implemented in OCaml. The OCaml library and examples were compiled in “unsafe” mode, that is, without array bounds and other safety checks—the C code does not perform these checks either. The results with safety checks are also available.

This conclusion seems reasonable as a first approximation, but several details of the analysis process and individual results show that the real situation is less clear-cut. For one, the running times of most of the examples are so short that accurate profiling is not possible, i.e., time and gprof simply show 0 seconds. The figures in the graph were obtained by modifying the examples to repeatedly execute their main functions. The number of repetitions varies per example since otherwise the slower examples take too long. The timings indicated by the dots and the axis at right are calculated by dividing the wall-clock time of each C version by the number of repetitions. All but six of the serial examples (red) run so fast that comparisons are made based on tens, or usually hundreds of repetitions and in some cases this amplifies factors other than the interface overhead. The slowest example, for instance, kin--ser--kinRoberts_fp is iterated nearly 200 000 times to achieve a significant wall clock time. This means creating and destroying many more data structures than usual for such code. In fact, about 25% of the runtime is spent in garbage collection, about 15% in allocating nvectors (10% in calloc alone), about 10% in freeing memory on the C heap, and about 15% calling printf. There is very little calculation in this example and thus bookkeeping predominates (and OCaml does more of it than C). Similar comments apply to the second slowest example, kin--ser--kinRoboKin_dns (10% in garbage collection and 30% in printf formatting numbers).

The running times of the parallel examples (lighter red) often vary considerably between different runs. Those with the highest variations—with the exception of idaHeat2D_kry_bbd_p—often have relatively long running times and the results are obtained in relatively few (< 10) iterations.

We were able to make our OCaml versions much faster (up to 4 times) by:

In summary, OCaml code using the Sundials solvers should almost never be more than 50% slower than the equivalent code written in C, provided the guidelines above are followed, and it should usually not be more than 30% slower. It is usually, however, faster to write and debug OCaml code thanks to automatic memory management, bounds checking on arrays, strong static type checking, higher-order functions, etcetera. Moreover, the Sundials/ML library offers a good comprise for programs combining symbolic manipulation and numeric calculation.

The graph above can be generated from the Sundials source by running

cd examples; make perf-intv.opt.pdf GC_AT_END=1 PERF_DATA_POINTS=40

Be sure to build Sundials with -DCMAKE_BUILD_TYPE=Release otherwise the underlying library is unoptimized. Sundials/ML should be configured with -unsafe.

References

  1. A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S. Woodward, “ SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers,” ACM Transactions on Mathematical Software, 31(3), pp. 363-396, 2005.
  2. T. Bourke, J. Inoue, and M. Pouzet, “Sundials/ML: interfacing with numerical solvers,” ACM Workshop on ML, Nara, Japan, 2016.
  3. T. Bourke, J. Inoue, and M. Pouzet, “Sundials/ML: Connecting OCaml to the Sundials Numeric Solvers,” EPTCS 285, pp. 101–130, 2018.
  4. X. Leroy, “Old Objective Caml site: Writing efficient numerical code in Objective Caml,” July 2002.

Acknowledgements

We gratefully acknowledge the support of the ITEA 3 project 11004 MODRIO (Model driven physical systems operation), Inria (Modeliscale), and the Departement d'Informatique de l'ENS.

This library benefits greatly from the OCaml Bigarray and MPI libraries, and from OCaml's optimized floating-point representations and compilation.

This documentation uses J. Protzenko's CSS stylesheet, and MathJax for rendering mathematics.

We are grateful for direct contributions to this library from

Indexes